LLM inference optimization: Speculative Decoding

Speculative decoding paper

Introduction

LLM inference is a sequential process where each new token is generated conditioned on the previously accumulated tokens - n iterations of LLM inference can’t be parallelized as the input of the current step depends on the output tokens generated by the previous step.

We make the following observations:

Inference is memory bound

The LLM inference process is inherently bottlenecked by the memory due to the auto regressive (generate one token at a time) nature. In simple terms it means that the wallclock time is dominated by data transfers(model weights, kv cache) as opposed to performing the actual matrix multiplies on GPU.

This implies we can get away with performing additional computations on GPU per memory access without impacting the wallclock time.

Additional reading for more context, please refer to these public blogs: blog by Horace He Transformer inference arithmetic

Not all tokens are created equal

Some tokens are easier to predict for the LLM than other tokens. Eg for code generation maybe curly braces after if statement, generation of stop words, conjunctions and other easier to predict words. For instance if you feed a output schema into LLM input query you know the fields of the output and corresponding tokens. In theory, it should be possible for a smaller model to predict those easier tokens and offload some computation from a larger model.

Speculative decoding

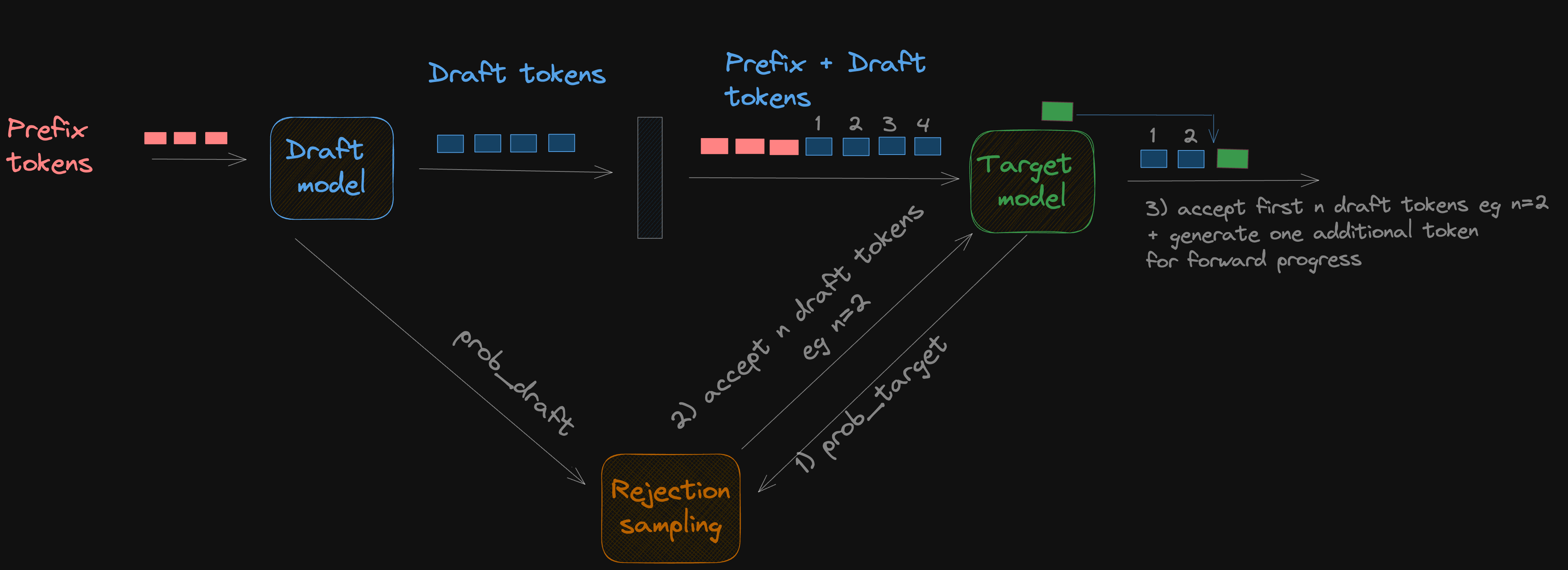
Speculative decoding technique exploits the above observations to speedup inference. We use a faster, smaller approximate model M_q to predict K lookahead tokens in parallel to the main larger, slower target model M_p.

The key observation is that this verification of K lookahead tokens can happen in a single forward pass. Additionally, forward pass for K tokens takes the same amount of wall clock time as a single token as we are memory bound in inference. We can potentially fast forward past multiple easy to guess tokens in a single iteration. The name of the technique comes from these lookahead tokens which are speculative in nature i.e. we first verify that the tokens guessed by the draft model are indeed correct.

The idea is inspired by speculative execution which is traditional technique employed in modern CPU processors where the processor is typically predicting branches speculatively to better overlap computation and memory access.

Notation

Token generation step consists of sampling from a probability distribution over the set of all possible tokens in the vocabulary. Normally this part is abstracted from the end user and we observe the generated tokens directly but for this discussion we would be operating on the probability distribution over tokens hence it is important to understand the notation.

Single step LLM inference:

1. x: Input token sequence
2. p(x): Output probability sequence eg output probability over all possible english letters(ignore tokenization here for sake of clarity). This probability distribution represents the probability of next token
3. x ~ p(x): Next token sampled from the above probability distribution Additionally we use p->target model, q->draft model
4. p(x) : Target model probability distribution
5. q(x) : Draft model probability distribution

Overview

1. Generate K lookahead tokens using M_q(draft model)
2. “Check” these generated lookahead tokens and accept them if it aligns with target model output distribution
3. The algorithm guarantees that sampling tokens from both models are theoretically equivalent - x ~ p(x) and x ~ q(x)

The advantage of above procedure is that algorithm enables the model to skip forward a few tokens in a single iteration if the tokens produced by draft model are deemed “good enough”. The hope is that in expectation, we are able to get more than 1 tokens accepted. In the paper they show 2-3x speedup on the target implementation.

Algorithm

Input: prefix tokens, target model and draft model. Output: One or more tokens

Pytorch implementation vllm repo

Draft & Target model inference

The first step is to generate speculative tokens using the draft model and extract probabilities from the target model.

1. Generate k tokens from the draft model. inputs : prefix tokens, draft model outputs: draft_token_ids: [batch_size, k], draft_probs: [batch_size, k, vocab_size]
2. Target model inference and get probabilities on the generated draft token ids for verification inputs: prefix tokens, target model, draft_token_ids outputs: target_probs: [batch_size, k, vocab_size].

Rejection sampling

First let’s break the accept/reject criteria step wise at the token level. Reminder q -> draft faster approximation model, p -> target model

If q(x) <= p(x) then we accept the token since the target model is more likely to generate this token and generally the speculative token stream emitted from the draft model is aligned with the target model token stream

If q(x) > p(x) : In this case we roughly want to reject tokens based on deviation/error roughly speaking if p(x) is only slightly lower than q(x) then we should probably accept the token since the error is fairly low. On the other extreme, if p(x) = 0 i.e. target model never emits the token x given the context, then we want to reject this token since the spec token stream is misaligned with the base token stream. This can be accomplished if we sample probabilistically (q(x)-p(x))/q(x)

The following code from vllm repo illustrates the idea

    def get_accepted(
            self,
            target_probs: torch.Tensor,  # [batch_size, k, vocab_size]
            draft_probs: torch.Tensor,  # [batch_size, k, vocab_size]
            draft_token_ids: torch.Tensor,  # [batch_size, k]
    ) -> torch.Tensor:
        r"""Create bool matrix over the proposed draft tokens. If
        True, then a token can be accepted, else it should be
        rejected.
        Returns a bool tensor of shape [batch_size, k] specifying which tokens
        are accepted.
        """
        batch_size, k, _ = draft_probs.shape
        # output shape [batch_size, k] gather corresponding probability values 
        # from vocab prob list based on selected draft token ids
        selected_draft_probs = torch.gather(draft_probs, 2, draft_token_ids.unsqueeze(-1)).squeeze(-1)

        # shape [batch_size, k] gather corresponding indices values
        selected_target_probs = torch.gather(target_probs, 2, draft_token_ids.unsqueeze(-1)).squeeze(-1)

        uniform_rand = torch.rand(batch_size,k)
        # p > q case mark as accepted, 
        # for q > p case, sample
        capped_ratio = torch.minimum(
            selected_target_probs / selected_draft_probs,
            torch.full((1, ), 1, device=target_probs.device))
        accepted = uniform_rand < capped_ratio
        return accepted

Generate extra token

In order to ensure forward progress for each iteration(in case we fail to get any token accepted) we generate one additional sample from the adjusted probability distribution p’(x) = \text{norm}(\max(0, p_{n+1}(x) - q_{n+1}(x)))

Roughly speaking, we are trying to sample a new frontier of the token space which lies further away from the frontier of the draft token space. For proof of this sampling algorithm, please refer to the appendix section in the paper

 # generate recovered tokens for case where samples get rejected
 difference = target_probs - draft_probs

 # reshape to prepare for sampling
 recovered_probs = difference.reshape(batch_size * k, vocab_size)

 # sample 1 id along the vocab axis
 recovered_token_ids = torch.multinomial(recovered_probs,num_samples=1)

 # reshape to get the original shape back
 recovered_token_ids = recovered_token_ids.reshape(batch_size, k)

Caveat

In the paper they evaluate gains on batch_size=1, however with much larger batch size, larger sequence size and generally higher utilization(compute bound regime) the gains from speculative decoding would be lower.