Implementing distributed transformer MLP layer in pytorch
by Shreyas Srivastava
Tensor parallel MLP is a common pattern in distributed transformer models. For instance Parallel mlp layer in GPT neox. The goal of this implementation is to simplify and understand how to implement this logic in distributed pytorch setup.
Typically we see the following kinds of parallelism in large transformer models.
Tensor parallelism
Splits the tensor computation across various GPU nodes. Typically this is used within a server datacenter node since this involves all reduce operations
Pipeline parallelism
Splits the sequential layers of the transformer model across different GPU nodes. This is analogous to the pipelining concept in computer architecture. Since implementing it requires cheaper communication cost(point to point instead of collective communication) it is typically implemented as we scale beyond a single host machine. More details
Data parallelism
Split the work across the batch axis and reduce the gradients using all-reduce operation.
Overview
Tensor parallel MLP block is common in high performance transformer architecture. We typically have a self attention block followed by MLP blocker interspersed with the dropout/layer norm layers. Here we focus on implementing the tensor parallel MLP layer.
By splitting the matrix, we can reduce the memory bandwidth requirements(memory bound) as we cut down the size of activation and weight matrix and hope to get a linear speedup by increasing the number of GPU’s.
We represent the input tensor using (B, T, D) where
B: Batch size
T: Sequence dimension
D: Hidden dimension
Matrix multiplication project up: Project from hidden dimensionDto4DieB,T,D -> B,T,4DNon linearity: Gelu/relu layer applied at the hidden dimension levelMatrix multiplication project down: Project back down from hidden dimension4DtoDieB,T,4D -> B,T,D
% Split the matrix-up weight vector along the column dimension.
% Note that splitting the input X along column and A along row
% doesn't work due to the non-linearity after this layer.
[Y1 Y2] = X [ A1, A2 ]
% apply the gelu independently across the tensor parallel degree
Z1,Z2 = gelu(Y1, Y2)
% split the second weight vector along the row
% eg if orig (m,n)*(n,k) -> (m, n/2) * (n/2, k) = (m,k)
[Z1 Z2 ] [ B1
B2 ]
Note that even though the dimension match in the final step
we still need to add the reduce the matrix across nodes
to get the final result.
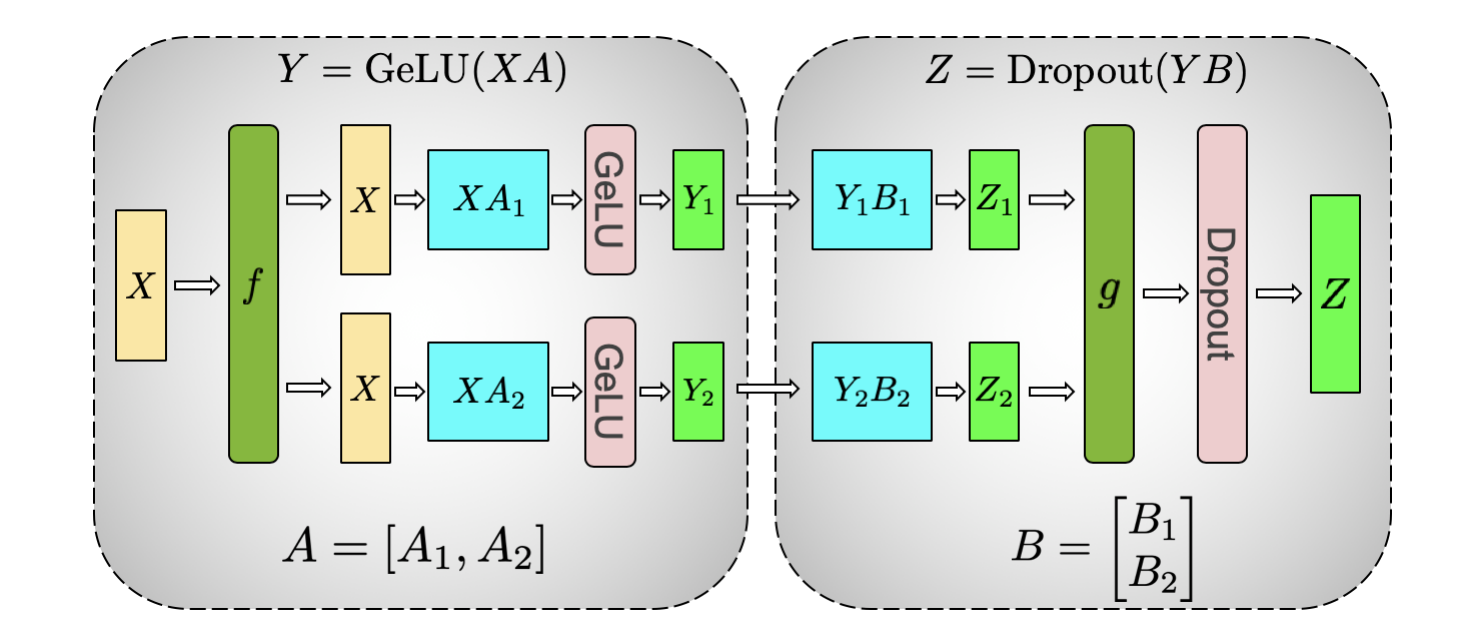
The following implementation is simplified as adapted from the Megatron code base simplified for educational purpose.
- We would be using a single host dual GPU setup to simplify the setup.
- We do NOT handle any weight initialization which would typically be required in real applications.
Setup distributed torch application
Initialize the simplified torch distributed setup to enable collective communications. This is covered in more detailed in the official pytorch guide
dist_launcherspawns multiple processes and handles the synchronization loopdist_initsets up the distributed process group which is used for collective communication ops such as all-reduce, all-to-all etc.
We can extend this simple setup as a skeleton for the final implementation
import os
import torch
from torch.multiprocessing import Process, Manager
def dist_init(rank, num_procs, run_func, *func_args, **func_kwargs):
"""Initialize torch.distributed and execute the user function."""
os.environ["MASTER_ADDR"] = "localhost"
os.environ["MASTER_PORT"] = "8081"
os.environ["LOCAL_RANK"] = str(rank)
os.environ["RANK"] = str(rank)
os.environ["WORLD_SIZE"] = str(num_procs)
os.environ.pop("NCCL_DEBUG", None)
init_method = 'tcp://'
init_method += os.environ["MASTER_ADDR"] + ':' + os.environ["MASTER_PORT"]
torch.distributed.init_process_group(
backend="nccl",
world_size=num_procs,
rank=rank,
init_method=init_method)
if torch.cuda.is_available():
torch.cuda.set_device(rank)
func_args = (rank,) + func_args
run_func(*func_args, **func_kwargs)
# make sure all ranks finish at the same time
torch.distributed.barrier()
# tear down after test completes
torch.distributed.destroy_process_group()
def dist_launcher(num_procs, run_func, *func_args, **func_kwargs):
"""Launch processes and gracefully handle failures."""
# Spawn all workers on subprocesses.
processes = []
manager = Manager()
queue = manager.Queue()
func_args = (queue,) + func_args
for local_rank in range(num_procs):
p = Process(target=dist_init,
args=(local_rank, num_procs, run_func, *func_args),
kwargs=func_kwargs)
p.start()
processes.append(p)
# Now loop and wait for a test to complete. The spin-wait here isn't a big
# deal because the number of processes will be O(#GPUs) << O(#CPUs).
any_done = False
while not any_done:
for p in processes:
if not p.is_alive():
any_done = True
break
# Wait for all other processes to complete
for p in processes:
p.join(200)
failed = [(rank, p) for rank, p in enumerate(processes) if p.exitcode != 0]
for rank, p in failed:
# If it still hasn't terminated, kill it because it hung.
if p.exitcode is None:
p.terminate()
print(f"Worker {rank} hung.")
if p.exitcode < 0:
print(f"Worker {rank} killed by signal {-p.exitcode}")
if p.exitcode > 0:
print(f"Worker {rank} exited with code {p.exitcode}")
if not any(failed):
activations = queue.get()
gradients = queue.get()
else:
activations = None
gradients = None
return activations, gradients
We can set up a dummy test loop like below which should print the output on the two processes. We will extend this harness later on.
def dummy():
rank = dist.get_rank()
world_size = dist.get_world_size()
print(torch.cuda.get_device())
print(rank)
if __name__=='__main__':
torch.multiprocessing.set_start_method('spawn')
dist_launcher(2,dummy)
Column parallel layer
[Y1 Y2] = X [ A1, A2 ]
The forward pass is straightforward as we simply need to need to output the matrix multiplication result corresponding to split column weight matrix.
However, in the backward pass gradient all-reduce op is needed to sum the gradient contributions from the branches going back from X * A1 and X * A2. In order to override the backward pass behavior, we will need to implement the torch.autograd.Function function and override the backward pass.
import torch
import torch.nn as nn
from torch.cuda.amp import custom_fwd, custom_bwd
class LinearColumnWithGradReduce(torch.autograd.Function):
"""See linear_with_grad_accumulation_and_async_allreduce"""
@staticmethod
@custom_fwd
def forward(ctx,input,weight,bias):
ctx.save_for_backward(input, weight)
output = torch.matmul(input, weight)
return output + bias
@staticmethod
@custom_bwd
def backward(ctx, grad_output):
# grad_output is (batch, T, output_size_partition)
# input is (batch, T, input_size_partition)
input, weight = ctx.saved_tensors
# (batch, output_size_partition) * (output_size_partition, input_size) -> (batch, input_size)
# (batch, T, input_size) = (batch, T, 1) * (1, input_size)
grad_input = grad_output.matmul(weight.T)
# Asynchronous all-reduce
handle = torch.distributed.all_reduce(grad_input, async_op=True)
# collapse first two dimensions
grad_output = grad_output.view(-1, grad_output.size(-1))
input = input.view(-1, input.size(-1))
# (batch*T, output_size_partition) * (batch*T, input_size_partition) -> (output_size_partition, input_size_partition)
grad_weight = grad_output.t().matmul(input).T
grad_bias = grad_output.sum(dim=0)
handle.wait()
return grad_input, grad_weight, grad_bias
class ColumnParallelLinear(torch.nn.Module):
"""Linear layer with column parallelism.
The linear layer is defined as Y = XA + b. A is parallelized along
its second dimension as A = [A_1, ..., A_p].
"""
def __init__(self, rank, weight_per_rank, bias_per_rank):
super(ColumnParallelLinear, self).__init__()
self.rank = rank
self.weight = nn.Parameter(weight_per_rank)
self.bias = nn.Parameter(bias_per_rank)
def forward(self, input_: torch.Tensor):
return LinearColumnWithGradReduce.apply(input_, self.weight, self.bias)
Relu layer
Relu layer should continue to work as expected normally
Row parallel layer
In the Row Parallel Layer, the weight matrix is split along the row dimension. The implementation is very similar to column parallel with couple of differences:
- All reduce is required on the forward pass to accumulate partial results from row level matrix multiplication combined with previous column result
- Backward pass doesn’t require any all reduce as the gradients don’t need to be combined on the backward pass.
import torch
import torch.nn as nn
from torch.cuda.amp import custom_fwd, custom_bwd
class LinearRowWithTensorReduce(torch.autograd.Function):
@staticmethod
@custom_fwd
def forward(ctx,input,weight,bias,rank):
ctx.save_for_backward(input, weight)
if rank == 0:
output = torch.matmul(input, weight) + bias
else:
output = torch.matmul(input, weight)
# all reduce along tensor parallel dimension
torch.distributed.all_reduce(output)
return output
@staticmethod
@custom_bwd
def backward(ctx, grad_output):
input, weight = ctx.saved_tensors
# (batch, T, input_size) * (output_size_partition, input_size) -> (batch, T, input_size)
grad_input = grad_output.matmul(weight.t())
grad_output = grad_output.view(-1, grad_output.size(-1))
input = input.view(-1, input.size(-1))
# (output_size_partition,batch*T) * (batch*T, input_size) -> (output_size_partition, input_size)
grad_weight = input.T.matmul(grad_output)
grad_bias = grad_output.sum(dim=0)
return grad_input, grad_weight, grad_bias, None
class RowParallelLinear(torch.nn.Module):
"""Linear layer with row parallelism.
its second dimension as Z = X [ Y1
Y2 ]
"""
def __init__(self, rank, weight_per_rank, bias_per_rank):
super(RowParallelLinear, self).__init__()
self.rank = rank
# weight_per_rank is (output_size_partition, input_size)
self.weight = nn.Parameter(weight_per_rank)
# bias_per_rank is (input_size,)
self.bias = nn.Parameter(bias_per_rank)
def forward(self, input_: torch.Tensor):
# input_ is (batch, T, output_size_partition)
return LinearRowWithTensorReduce.apply(input_, self.weight, self.bias, self.rank)
Putting it together
Putting together the column and row parallel MLP as described above and wrapping up in a runnable function across each GPU machine.
We add some logic here to trigger the backward pass and calculate gradients against a dummy loss function. Finally, we shuttle the activations from the final layer and gradients on the input back to the parent process.
def run_parallel_mlp(rank, queue, weight_layer1, bias_layer1, weight_layer2,bias_layer2, x, dummy_labels):
rank = dist.get_rank()
device_id = torch.cuda.current_device()
# Split and move weights and biases to the current device
weight_per_rank_layer1 = split_tensor(weight_layer1, OUTPUT_SIZE_PER_PARTITION, -1, rank)
bias_per_rank_layer1 = split_tensor(bias_layer1, OUTPUT_SIZE_PER_PARTITION, -1, rank)
weight_per_rank_layer2 = split_tensor(weight_layer2, OUTPUT_SIZE_PER_PARTITION, 0, rank)
# Create and apply ColumnParallelLinear module
myColParallelModule = ColumnParallelLinear(rank, weight_per_rank_layer1,
bias_per_rank_layer1).to(device_id)
x_cuda = x.to(device_id).requires_grad_(True)
out_layer1_per_rank = myColParallelModule(x_cuda)
# Apply ReLU activation
relu = nn.ReLU().to(device_id)
out_relu_per_rank = relu(out_layer1_per_rank)
# Create and apply RowParallelLinear module
rowParallelLinearModule = RowParallelLinear(rank, weight_per_rank_layer2, bias_layer2).to(
device_id)
out_layer2 = rowParallelLinearModule(out_relu_per_rank)
# Compute loss and perform backward pass
loss = torch.square(out_layer2 - dummy_labels.to(device_id)).sum()
loss.backward()
# Save outputs and gradients if rank is 0
if rank == 0:
queue.put(out_layer2.cpu().clone().detach())
queue.put(x_cuda.grad.clone().cpu().detach())
Test forward and backward pass
To verify that our parallel MLP implementation works as expected, we compare the activations and gradients against the standard MLP layer implementation. as previously mention, we can extract the activation and gradients using torch distributed queue
if __name__=='__main__':
mp.set_start_method('spawn')
################################################
# Init the weights in the main function
# and pass it to the child processes
# to enable checking against the baseline MLP
################################################
weight_layer1, bias_layer1, weight_layer2, bias_layer2, x, dummy_labels = init_tensors()
# Run the baseline MLP to verify parallel MLP logic
base_mlp = BaseMLPLayers(weight_layer1, bias_layer1, weight_layer2, bias_layer2)
# we are doing some unsual stuff here, cloning the tensor to avoid backprop
# through the distributed code path
clone_x = x.clone().requires_grad_(True)
# check forward pass output with base MLP
base_output = base_mlp(clone_x).cpu()
# Run the distributed code path including Parallel MLP
activations, grad_actual = dist_launcher(2,run_parallel_mlp,weight_layer1,bias_layer1,weight_layer2,
bias_layer2, x, dummy_labels)
print(base_output[0][0][0:10])
print(activations[0][0][0:10])
assert torch.allclose(base_output, activations, atol=1e-4)
print("Parallel MLP output matched with base MLP output")
# dummy loss function
loss = torch.square(base_output-dummy_labels).sum()
loss.backward()
# calculated gradient for input
grad_expected = clone_x.grad
print(grad_expected[0][0][0:10])
print(grad_actual[0][0][0:10])
# gradients have lower tolerance for some reason
assert torch.allclose(grad_expected, grad_actual, atol=1e-1)
print("Parallel MLP gradient matched with base MLP gradient")
$ python run.py
tensor([-13.2234, 14.5334, 50.0128, 59.7735, 36.3903, -54.5164, 21.5732,
-47.9403, -8.4203, 57.2465], grad_fn=<SliceBackward0>)
tensor([-13.2234, 14.5334, 50.0128, 59.7735, 36.3903, -54.5164, 21.5732,
-47.9403, -8.4203, 57.2465])
Parallel MLP output matched with base MLP output
tensor([-7869.1587, 1106.3701, 9856.4297, 1074.2012, -9341.9961, 23347.9883,
-5745.2598, 22844.5840, -3963.1760, 9396.2031])
tensor([-7869.1562, 1106.3760, 9856.4316, 1074.2002, -9341.9961, 23347.9922,
-5745.2598, 22844.5781, -3963.1763, 9396.2021])
Parallel MLP gradient matched with base MLP gradient